并查集回顾-

前言:我浅显的把他定义为可以解决类似寻找联通路和独立块之类的问题。今年再拾起来的时候，自己敲代码的时候已经有了一种生疏的感觉，可见定期多看看自己以前写过的代码，学过的算法时多么重要啊~所以写今天这篇博客一方面是再把刚刚写过的复盘巩固一下，另一方面方便日后再进行回顾，还有要是或多或少帮助到屏幕前额你，我也感到十分荣幸。

这次还是用一道入门题来回顾：(题目来自HDU-OJ)

Title

畅通工程

Problem Description

某省调查城镇交通状况，得到现有城镇道路统计表，表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要互相间接通过道路可达即可）。问最少还需要建设多少条道路？

Input

测试输入包含若干测试用例。每个测试用例的第1行给出两个正整数，分别是城镇数目N ( < 1000 )和道路数目M；随后的M行对应M条道路，每行给出一对正整数，分别是该条道路直接连通的两个城镇的编号。为简单起见，城镇从1到N编号。注意:两个城市之间可以有多条道路相通,也就是说 3 3 1 2 1 2 2 1 这种输入也是合法的当N为0时，输入结束，该用例不被处理。

Output

对每个测试用例，在1行里输出最少还需要建设的道路数目。

Sample Input

Sample Output

Java code:

import java.util.Scanner;

public class HDU_1232 {
    //寻找祖先方法
    static int find(int[] parent,int f){
        int r = f;
        while (parent[r]!=-1){
            r = parent[r];
        }
        int i = f,j;
        //路径压缩（解释请往下翻）
        while (i!=r){
            j = parent[i];
            parent[i] = r;
            i = j;
        }
        return r;
    }
    
    //联合方法
    static void union(int[] parent,int x,int y){
        int fx = find(parent,x);
        int fy = find(parent,y);
        if(fx != fy){
            parent[fx] = fy;
        }
    }
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        while (n != 0) {
            int m = sc.nextInt();
            int sum = 0;
            int[] parent = new int[n+1];
            //初始化祖先数组
            for(int i = 1;i<=n;++i){
                parent[i] = -1;
            }

            for (int i = 0; i < m; i++) {
                int x = sc.nextInt();
                int y = sc.nextInt();
                union(parent,x,y);
            }

            for (int i = 1;i <= n ;i++){
                if (parent[i] == -1){
                    sum++;
                }
            }

            System.out.println(sum-1);
            n = sc.nextInt();
        }
    }
}

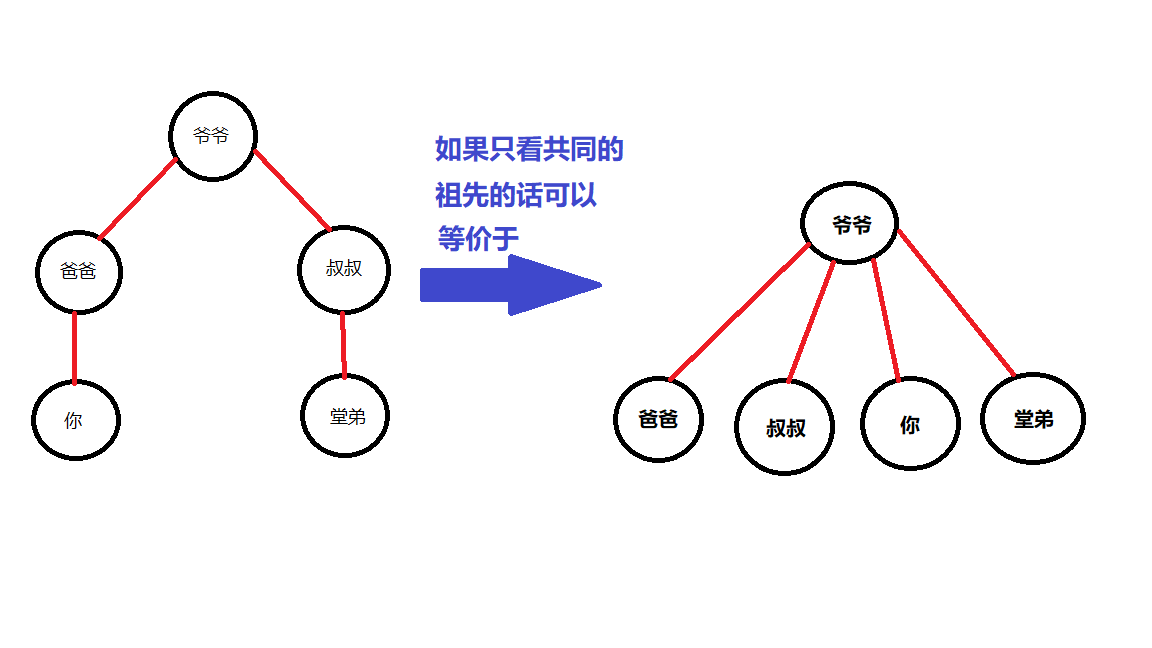
路径压缩解释图

「真诚赞赏，手留余香」

并查集回顾

TOC

Java code:

FEATURED TAGS

FRIENDS